We introduce the notion of Cross-Iteration Dependencies and briefly explain how one can statically resolve them.
We discuss a running example that serves as Motivation for Using TLS Parallelization.
We discuss Thread-Level Speculation (TLS) at a High Level and
We show a Naive Software-TLS Implementation.
We modify the naive TLS version in several key places to obtain a Lightweight Software-TLS Implementation.
We demonstrate how to use the PolyLibTLS Library to speculatively parallelize the running example, and
We conclude with a discussion of the PolyLibTLS performance w.r.t. the running example.
Finally, we list a set of references.
- true/flow dependency, a.k.a., read after write (RAW): a memory location is written in an iteration i and read in a following iteration j , i.e., i < j. True dependencies correspond to a producer-consumer relation between iterations, and eliminating them typically require algorithmic changes that are beyond the ability of the compiler.
- anti dependency, a.k.a., write-after-read (WAR): the (same) memory location is read in an iteration i and is updated in a following iteration j , i.e., i < j.
- output dependency, a.k.a., write after write (WAW): the same memory location is written in two different iterations.
- the access pattern of array a produces cross-iteration
true dependencies, because, for example, iteration
i=2 writes a(2) and iteration i=3
reads a(2). The computation of
acan be parallelized because it has the semantics of a prefix-sum computation with associative operator+, i.e., scan(op +, 0, [2..i]). This is however an algorithmic change that that a compiler will not be typically able to perform in a reliable fashion. - the access pattern of array b produces cross-iteration anti dependencies, because, for example, iteration i=2 reads b(3) and iteration i=3 writes b(3). If executed in out of order, iteration 2 might consume a value produced ``in the future'' by iteration 3, which violates the sequential semantics. This dependency can be resolved via renaming, i.e., copy array b to b_copy and replace the reads from b with the reads from b_copy.
- the access pattern of array c produces cross-iteration output dependencies, because any iteration of the outer loop writes (in the first inner loop) the first N elements of array c , i.e., c[1:N]. Furthermore, the second inner loop reads c[1:N] in every iteration of the outermost loop, and gives raise to all kinds of dependencies. At a first view it seem difficult to resolve the many dependencies on c , but this can be relatively-simply achieved via a compiler transformation called privatization: Note that all the reads of an outermost iteration are covered by writes in the same outermost iteration, and as such making each iteration operate of its own private copy of c would preserve the sequential semantics and resolve all dependencies on c . Since all iterations update the same subset of indices in c , then the last iteration updates the global storage, i.e., static last value.
- if X is a permutation of {0..N-1} then no cross-iteration dependencies exists,
- if X contains only one or two distinct values then frequent cross-iteration dependencies will manifest during execution because multiple iterations will work on the same row,
- if X contains random numbers in {0..N-1}, then the occasional cross-iteration dependency exists.
- strictly monotonic , or
- distinct, i.e.,
Xis a permutation of {0,..,N-1}. -
&Xdenotes the address of variableX, -
specST(&X, val, i)updates variableXto valuevalif this does not cause a dependency violation, and otherwise throws an exception, and -
specLD(&Y,i)returns the value ofY -
idenotes the iteration in which the update/read takes place and is used for bookkeeping. - Records that the current iteration (
itNr) has read from positionind, i.e.,LdVct[ind][itNr] = 1, and - Searches the store vector to find the highest iteration lower or equal to itself
that has written in
a(ind). - If such an iteration exists then the corresponding value is returned,
otherwise the data is read from global memory (
orig) - Records the to-be-updated value in private (shadow) storage,
i.e.,
ShVct[ind][itNr] = val, then - Records the information that the current iteration has written to
a(ind), i.e.,StVct[ind][itNr] = 1, and finally - It inspects the load vector (
LdVct[ind]) to check that no successor thread (i.e., executing iterations greater thanitNr) has read froma(ind). If the latter does not hold, it means that a successor iteration has read an incorrect value and a RAW dependency has been violated => ROLLBACK - can be composed to parallelize the target loop and
- can be tuned to take advantage of specific access-patterns of the target loop.
- The ``hash'' function maps global memory locations to indexes of the speculative-memory load and store vectors.
- To fix the asymptotic time behavior, we maintain only one element in the load/store vectors corresponding to one equivalence class, rather than P as in previous work.
- Each thread operates directly on the global memory locations,
i.e., in-place updates , but prior to an update it stores
the held value in thread private storage
ShBuff[p]. - In Figure,
Wdenotes the maximal number of per-loop-iteration writes, andShBuff[p]can be implemented as a vector (of dynamic size). - For each equivalence class
i,LdVct/StVct[i]holds the maximal iteration number that has read/written an address belonging to equivalence classi, i.e.,hash(addr) = i. It follows that: - For a speculative-load operation: if the value inscribed in
StVct[i]is greater than the current iteration performing the write (itNr) then there are two write-operations that have not occurred in program order, i.e., a WAW dependency violation has been discovered. - For a speculative-load operation: if the value inscribed in
LdVct[i]is greater than the current iteration performing the write (itNr) then a successor iteration has read an incorrect value, i.e., the successor iteration should have read the value produced by the current iteration, hence a RAW dependency violation has been discovered. - Otherwise, the value hold in
addris saved in thread's private storage (ShBuff), the target address is updated to hold the new valuenew_val, andspecSTsucceeds. - If a RAW, WAW, WAR violation is discovered then the master thread will
service a rollback procedure, in which the updates of all threads
(up to and including the master) are rolled back based on the
ShBuffinformation, and speculation is restarted. - The memory space overhead is proportional with the cardinality of the ``hash'' function. Under regular accesses, the memory overhead can be as small as P.
- For example, with the loop above,
hash(a) = a % Pof cardinality P would not introduce any false positive dependencies if iterations {p, p+P, p+2*P, ...} are executed on processor `p', and would provide ideal cache behavior if the elements ofLdVct/StVctdo not share cache-lines. - The time overhead of
specLD/STis constant, i.e., does not depend on P. - While, for simplicity, the pseudo-code requires
specLD/SToperations to execute atomically, the full paper presents an implementation that, for X86 processors, is both lock free , i.e., no CAS instructions, and sequential consistent , i.e., no memory fences. - Obviously, the in-place implementation does not exhibits the non-scalable behavior observed sometimes for implementations that use a serial-commit phase.
- The memory is partitioned according to the variables that are used, and dependencies on addresses in each partition are tracked via a TLS implementation that is tuned to the access patterns of the corresponding variables.
- A speculative-thread manager is declared. Its task is to coordinate the execution of threads and to implement the rollback-recovery procedure.
- The programmer then defines a customized speculative thread that executes a set of consecutive iterations of the original loop, where the problematic accesses are disambiguated via TLS.
- Finally, the original loop is replace with glue code that creates the speculative threads, registers them to the thread manager, spawns them and awaits the termination of the speculative code.
- The idea is to put all addresses corresponding to a row
into the same equivalence class, because an outer-iteration
accesses elements in the same row. It follows that a
speculative read/write on any element of the
row uses the same entry in the speculative storage, e.g.,
load/store/shadow vectors. The cardinality
of the ``hash'' function is N, i.e., the number of rows:
hash : [mat, &mat+N*M) -> [0,N-1],
hash(a) = ( (a-mat) div (4*M) ) mod N
where `div' and `mod' stand for integer division and modulo, respectively, andmatcorresponds to the start address of the matrix. ClassHashSeqPow2uses fast arithmetic, hence the use of logarithm in the code. - We use the previous step to build a SpLIP instance that is
tuned to the access patterns of
mat:-
IPm_coreexports the basic implementation of the speculative load and store operations and its instancem_coreuses the hash function to cluster accesses, -
IPmextends the core functionality with support for private buffering and rollback recovery, e.g.,ENTRY_SIZE=1corresponds to the size of the thread-private-write buffer, which is an overestimate of the number of updates performed by an iteration. -
Finally,
ip_m.setIntervalAddr(...)sets the lower and upper bounds of the global-memory partition protected by the current TLS instance.
-
-
Similarly an instance of the SpecRO model, named
ro_mis created. The intent is that it will protect any address that does not fall in the range of address of the matrixmat. -
Finally, a ``unified-speculative instance'' is built, i.e.,
UMeg. Combining the TLS instances is achieved by creating a chain ofUSpModelinstantiations, in whichUSpModelFPdenotes the end of the chain, and the previous-innermost TLS instance is the default one. By ``default'' we mean that it protects the memory space that was not covered by the previous partitions.
- If a 'specLD/ST' is invoked directly on a TLS instance and it is not within the corresponding memory-partition bounds, then it causes a rollback.
- If a 'specLD/ST' is invoked on the "unified" instance 'umm' then the memory partitions are checked in the order in which they have been defined in 'USpModel', until the right one is find, where the last instance is the default one, i.e., covers the rest of the memory.
- The first type parameter is the ``self'' (currently declared) type,
i.e.
ThManager, and allows to specialize (if needed) the default implementation ofMaster_AbstractTM. - The second and third parameters are the
unified-speculative-memory partitions type and instance,
i.e.,
ummof typeUMeg. They are needed for the implementation of the rollback-recovery procedure. - The fourth parameter is the number of speculative threads that are used for loop parallelization, and the fifth parameter is not currently used, hence 0.
-
The last type parameter provides additional instructions about
how to parallelize the code. For example,
NormalizedChunks<ThManager, UNROLL>means: stripmine the original loop by anUNROLLfactor, where the resulted big iterations are dynamically scheduled for execution on the speculative threads. In our caseUNROLLis 1 because the outer iteration has enough granularity, i.e., it executes an inner loop of count M. - The constructor
Thread_Max(which should also be hidden from being used directly by the programmer) - Initialization for the variables used inside the loop,
e.g.,
initVarsinitializesjto 0. Herejdenotes the outermost loop index. - The test for the end-of-loop condition, i.e.,
end_conditionreturn true if the outermost loop indexjbecomes greater or equal to the loop countN. -
updateInductionVarscomputes the outermost loop indexthis->jcorresponding to the start of a strip-mined (unrolled) iterationthis->id. Note that the code is a bit awkward because for obscure reasons the numbering of big iterations starts fromNUM_THREADSrather than from 0, and as such one has to take the differenceid - ttmm.firstID()when computingj. -
iteration_bodyimplements the body of the original loop where the ``normal'' loads and stores from/to global memory have been replaced with calls to the high-level functionsspecLD/STthat implement TLS's dependency tracking. -
Finally,
non_spec_iteration_bodyis used by the thread manager when servicing a rollback, and it is supposed to be identical withiteration_bodyexcept that it uses non-speculative loads and stores, i.e., direct access to global memory. - reading
X[j]is performed via a call to the unified speculative-memory modelumm, i.e.,umm.specLDslow(&X[this->j],this). This call checks the ranges of all memory partitions until it finds one that fits and services the speculative load operation via the TLS instance that is associated with that memory partition. In our case that is a SpecRO implementation. -
Read and write accesses to the matrix elements are performed
via
specLD/SToperations that are implemented at the speculative-thread level and which are optimistically dispatched to the TLS implementation indicated by the type parameters of the call, e.g.,specLD<IPm, &ip_m>(&row[i]). This optimizes the dispatch time, but if the read address does not belong to the specified partition then a false-positive dependency violation will be signaled. - to create the speculative threads, i.e.,
allocateThread<SpecTh>(i, 64), whereistands for the initial thread identifier, and 64 is denotes the padding size - to register the speculative threads to the thread manager, i.e.,
ttmm.registerSpecThread(thr,i), and - to ask the thread manager to execute the speculative code,
i.e.,
ttmm.speculate<Thread_Max>(); - If
MODEL_LOCKis defined thenspecLD/STuses compare-and-swap (CAS) instructions to implement load/store atomicity (spinlock). - If
MODEL_FENCEis defined thenspecLD/STuses a CAS-free implementation, i.e., no locks, but memory fences are required. - If
MACHINE_X86_64is defined thenspecLD/STuses neither CAS nor memory fences, but may introduce the occasional false-positive dependency. Note that correctness is guaranteed only for X86 machines, which implement the least relaxed memory-sequential consistent model. - the non-speculative sequential time is 1787946 ns,
- the speculative time on 1 thread is 6156013 ns, and
- the speculative time on 6 thread is 1368638 ns.
-
L. Rauchwerger and D. Padua.
"The LRPD Test: Speculative Run-Time Parallelization of
Loops with Privatization and Reduction Parallelization",
IEEE Trans. on Parallel and Distributed System,
10 No 2(2), pp 160-199, Feb 1999.
-
P. Rundberg and P. Stenstrom.
"An All-Software Thread-Level Data Dependence
Speculation System for Multiprocessors.",
Journal of Instruction-Level Parallelism, 1999.
-
Cosmin E. Oancea, Alan Mycroft and Tim Harris.
"A Lightweight In-Place Implementation for
Software Thread-Level Speculation",
21st ACM Symposium on Parallelism in Algorithms and Architectures (SPAA'09),
August 2009, Calgary, Canada.
PDF
-
Cosmin E. Oancea, Alan Mycroft and Stephen M. Watt.
"A New Approach to Parallelising Tracing Algorithms",
International Symposium on Memory Management (ISMM'09),
June 2009, Dublin, Ireland.
PDF
-
Cosmin E. Oancea and Alan Mycroft.
"Set-Congruence Dynamic Analysis for Software Thread-Level Speculation",
21st Int. Lang. and Compilers for Parallel Computing (LCPC'08),
August 2008, Edmonton, Canada.
PDF
-
Cosmin E. Oancea and Alan Mycroft.
"Software Thread-Level Speculation: an Optimistic Library Implementation",
International Workshop on Multicore Software Engineering (IWMSE'08),
pp 23-32 (ACM Digital Library), May 2008, Leipzig, Germany.
PDF
-
Cosmin E. Oancea and Lawrence Rauchwerger.
"A Hybrid Approach to Proving Memory Reference Monotonicity",
24th Int. Lang. and Compilers for Parallel Computing (LCPC'11),
LNCS, Vol 7146, pp 61-75, Sept 2013.
PDF
-
Cosmin E. Oancea and Lawrence Rauchwerger.
"Logical Inference Techniques for Loop Parallelization",
33rd ACM-SIGPLAN Conf. on Prog. Lang. Design and Implem. (PLDI'12),
pp 509-520, June 2012.
PDF
Cross-Iteration Dependencies
The static approach to automatic (loop) parallelization has been to prove at compile time that executing iterations of a loop in parallel always gives the same result as the sequential execution of that loop.This invariant is typically modeled via dependence analysis, and the compiler attempts to resolve or to prove the absence of dependencies that are carried across iterations . Dependencies are of three kinds:
a(1) = 0
DO i = 2, M
a(i) = a(i-1) + i
b(i) = ... b(i+1) ...
DO j = 1, N
c(j) = ...
ENDDO
...
DO j = 1, N
d(j,i) = ... c(i) ...
ENDDO
ENDDO
Consider the loop above
Thread-Level Speculation (TLS) Motivation
In practice, there are many factors that significantly hinder the ability of static analysis to prove loop independence: symbolic constants, complex control flow, quadratic or indirect-array indexing, object/pointer aliasing etc.
// X -> indirect array of size N and elements in {0..N-1}
// mat -> a NxM matrix, i.e., 2-dimensional (full) array of size N*M
void computeArr2D(int* X, float* arr2d) {
for(int i=0; i < N; i++) {
float* row = &mat[ X[i]*M ];
float sum = 0.0;
for(int j=0; j < M; j++) {
if (j < M-32) {
sum += (row[j] + row[j + 32]) / (row[j + 32] + 1.0);
} else {
sum += (row[j] + row[j - 32]) / (row[j - 32] + 1.0);
}
}
row[0] += sum;
}
}
The contrived code example above uses the indirect array
X , which
contains integral elements in [0,N-1], to select a row of an NxM matrix,
denoted mat , and updates the first element of that row.
The first-element update depends only on the elements of that (same) row,
and is implemented by the inner loop. The content of the indirect array
X , which we assume statically unknown, dictates the
pattern of cross-iteration dependencies of the outer loop:
X are:
X
are strictly increasing, and if so then the outer loop can be safely parallelized.)
However, if the elements of X are random in {0..N-1}, then
the outer loop will exhibit a significant amount of parallelism, albeit the
occasional cross-iteration dependency violation may still occur.
This example suggests that there are cases in which (static) compiler analysis
is too conservative, and a more dynamic treatment of dependencies could be
beneficial, i.e., exploiting ``partial'' parallelism. Thread-Level Speculation (TLS) Introduction
Thread-Level Speculation (TLS) is a parallelization technique that allows loop iterations to be executed (optimistically) in parallel even in the presence of cross-iteration dependencies, which are tracked and fixed at runtime. Rauchwerger and Padua have pioneered the TLS domain in the seminal work that proposed the LRPD test.TLS exploits code regions that dynamically expose a good amount of parallelism but for which static analysis fails to guarantee safety. Under TLS threads execute out of order (but are well-localized), and use software/hardware structures, referred to as "speculative storage", to record the necessary information to track the inter-thread dependencies and to revert to a "safe point" and restart the computation upon the occurrence of a dependency violation (a.k.a., "rollback recovery").
Hardware TLS solutions use an extended cache-coherency protocol to support dependency tracking and the rollback mechanism. They are typically more effective than software solutions but (i) the limited speculative storage may limit their ability to exploit coarser levels of parallelism, and (ii) they are not mainstream.
With software TLS, accesses to variables that cannot be statically disambiguated -- i.e., that may violate the sequential dependencies -- are replaced with calls to functions that simulate the cache-coherence protocol of hardware TLS solutions. For example, the assignment
X = Y is replaced with
specST(&X, specLD(&Y,i), i))
where
When does the commit take place?
The thread executing the lowest-numbered iteration is known as the "master" thread. The "master" thread encapsulates both the correct sequential state and control-flow. It follows that a thread waits to become "master" and at that point it is safe to commit its speculative updates to global/shared memory. Since the master thread always successfully commits, progress is guaranteed. In addition the "master" thread typically services the rollback procedure when it discovers that a successor thread has violated a dependency. The rollback procedure typically involves clearing the speculative metadata and restarting all (successor) speculative threads.
Naive Software-TLS Implementation
For explanation purposes we use a very-simplified/naive variant of Rundberg & Stenstrom all software TLS implementation. First, read and writes to data-structures (arrays) that may cause dependency violations under parallel execution are protected with speculative support, i.e., a read/write from array a is re-written via specLD/ST calls:
DO i = 1, N DO i = 1, N
a(b(i)) = a(c(i)) <-> val = specLD(b(i), i)
specST(c(i), val, i)
ENDDO ENDDO
WORD specLD(int ind, int itNr) { void specST( int ind, WORD val, int itNr ){
LdVct[ind][itNr] = 1; ShVct[ind][itNr] = val;
int i = highest StVct[ind][itNr] = 1;
index marked
in StVct[ind] <= itNr; if( exists i > itNr with LdVct[ind][i]==1 )
Mark_Dep_Exc(i);
if(i>=0) return ShVct[ind][i];
else return orig;
} }
WHERE the original array a has been replaced with the data-structure
depicted below: each element of the original a corresponds to a load vector (LdVct),
a store vector (StVct), and a shadow vector (ShVct) of size N,
where N denotes the number of loop iterations. A speculative read (
specLD) from a(ind):
specST) to a(ind):
Upon ROLLABCK, when the current thread becomes master, it commits its updates to non-speculative storage (i.e.,
orig field) and clears/resets the
speculative metadata of all successor threads.
Note that if the current thread does not become master, then there has to be a
predecessor thread that has become master and services the rollback.
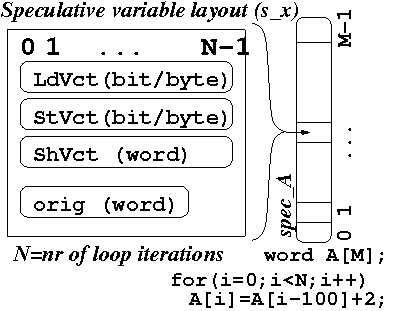
The naive implementation above exhibits a large (speculative) memory overhead: O(N^2) memory is used to speculate over an array of size N. The typical optimization is to have only a window of iterations executed concurrently (a small factor of P, the number of processors). This reduces the memory overhead to O(P*N) and the complexity of
specLD/ST to O(P), since
a speculative load (store) would need to check at most P entries in StVct/LdVct to
find the to-be-returned value (or to identify a potential RAW dependency violation). Such an implementation has the advantage of being accurate, in that it exhibits no false positive violations and WAW and WAR dependencies are inherently enforced, i.e., they are never the source of dependency violations/rollbacks. There are however several significant shortcomings:
First, the significant memory overhead, proportional with P*N, where N is the array size and P is the number of processors, may pressure the memory-hierarchy system and may degrade performance.
Second, the commit phase is serial, since a thread need to become master in order to commit its updates to non-speculative storage. The consequence is that speedup will not scale beyond a fixed number of processors.
Third, at least the speculative store operation has worst-case complexity O(P), which means, with our example, that we have O(N*P) parallel work and O(N*P/P)=O(N) depth, i.e., asymptotically we do not improve over sequential execution.
Lightweight Software-TLS Implementation
Our work in this context has taken the perspective that rather than employing one over-arching (TLS) implementation for all loops, one can exploit the flexibility of software TLS to engineer a family of lightweight (TLS) implementations thatFor example, a loop in which the elements of an array are mostly read, e.g., written only in case of error, can be effectively protected by the simple TLS implementation in which specST always signals that a dependency violation has occurred and specLD simply returns the corresponding value from global memory. Note that when speculation succeeds, i.e., no write accesses occur at runtime, this implementation exhibits zero memory-space and time overhead, as no speculative storage is required and no extra operations are performed. We name this implementation SpecRO.
Similarly, as with the loop below, it might happen that a statically unanalysable array exhibits at runtime a regular-access pattern, e.g., when `b(i)' and `c(i)' are the identity function in the loop below. In these cases it certainly feels that maintaining a speculative storage proportional with N*P is excessive. For example, if thread `p ∈ {0,..,P-1}' executes iterations in '{p, p+P, p+2*P, ..}', then one can map the indexes of `a' into `P' equivalent classes, e.g., equivalence class p contains indexes in '{p, p+P, p+2*P, ..}'. This seems to imply that a speculative memory of size proportional with (only) `P', rather than `N*P', is required to efficiently parallelize the targeted loop.
DO i = 1, N b(i) = i DO i = 1, N a(b(i)) = ... ------------> a(i) = ... ... = ... a(c(i)) ... c(i) = i ... = a(i) ENDDO ENDDO
In essence, while a lot of (important) previous work has looked at how to optimize the original code/loop for a given TLS implementation, we took the orthogonal perspective in which we explore the equally important direction of tunning the TLS implementation to take advantage of the access-patterns exhibited by the targeted loop.
The immediate question is how to design a tunable TLS implementation? The simple answer is that we introduce a ``hash'' function that splits the global (non-speculative) memory space into equivalence classes, and the TLS implementation uniformly handles these equivalence classes rather than individual memory locations, i.e., a read/write into a memory location is conservatively interpreted as a read/write from each memory location in the corresponding equivalence class.
It follows that our implementations trades off the (hopefully) occasional false-positive violation for a small speculative storage exhibiting memory-friendly cache layout. The idea is that the latter properties would allow the speculative load/store operations to execute at a speed close to that of arithmetic operations, which will make the TLS-time overhead relatively small in comparison with the "original" code that typically "suffers" negative memory-hierarchy effects, such as cache misses, etc.
We demonstrate this perspective by discussing such a lightweight, in-place TLS implementation, named SpLIP . The full paper can be found here. The Figure below shows the speculative storage layout:
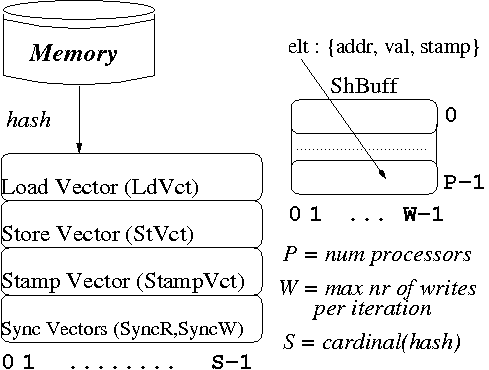
atomic WORD specLD( atomic void specST(
volatile WORD* addr, volatile WORD* addr,
int itNr ) { WORD new_val, int itNr) {
1 int i = hash(addr); 1 int i = hash(addr);
2 if(LdVct[i] itNr)
4 WORD val = *addr; 4 throw Dep_Exc(itNr-1);
5 if(StVct[i]<=itNr) 5 StVct[i] = itNr;
6 return val; 6 save( addr, *addr,
7 else throw StampVct[i]++ );
8 Dep_Exc(itNr-1); 7 *addr = new_val;
} 8 WORD load = LdVct[i];
9 if(load > itNr)
10 throw Dep_Ex(itNr-1); }
The load ( specLD ) operation receives as parameters the original to-be-read memory location, i.e.,
addr, and the iteration that
is performing the read operation, i.e., itNr.
The store ( specST ) operation receives
in addition the value new_val that the memory location addr
is to be updated to. The intuition behind the implementation is:
Principal observations are:
In essence, the above in-place implementation enables better scalable behavior (in number of processors that contribute to speedup), and features constant-time load/store operations (i.e., overhead not proportional with 'P'), but all RAW, WAR, and WAW dependencies may cause rollbacks. Furthermore, the use of the 'hash' function trades off potential false-positive violations for a small speculative storage with friendly cache layout. For example, even under non-regular accesses, e.g., Barnes-Hut, reducing the cardinality of the hash function from 2^{21} to 2^{14} corresponds to a significant increase in speedup from 2.84x to 5.29x on eight processors, respectively, where the optimal speedup, i.e., without TLS support is 7.38x.
Ideas about how to implement a dynamic analysis that would compute an effective hash function are reported here . We have observed that the in-place implementation is not suitable for all cases. For example if the loop exhibits WAW dependencies then a serial-commit model is more useful, due to its ability to naturally handle the WAW dependences. If the array is only occasionally written then perhaps the SpecRO implementation is the most efficient one.
Moreover, one array used in the loop may be best protected under one TLS implementation, e.g., SpLIP or SpecRO, while another array may be best protected under a serial-commit implementation, e.g., named SpLSC . The next section demonstrates the use of the PolyLibTLS library, which is designed to enable programs to be parallelized via such a compositional use of instances of TLS implementations.
Using PolyLibTLS Library to Parallelize the Running Example
The implementation of the library, together with some applications parallelized with it can be found at git@github.com:coancea/PolyLibTLS.git and the corresponding papers can be found in the Reference Section [3-6].PolyLibTLS makes heavy use of template meta-programming to allow a reasonably convenient way of writing TLS code without compromising performance. The implementation of the library is available in folder 'PolyLibTLS/LibTLS' and a demonstrative example, explained in this Section, is located in folder 'PolyLibTLS/Demo'.
This section shows how to apply thread-level speculation to our motivating example. We have already discussed its (dataset-sensitive, cross-iteration) dependency patterns in a previous section.
// X -> indirect array of size N and elements in {0..N-1}
// mat -> a NxM matrix, i.e., 2-dimensional (full) array of size N*M
for(int i=0; i < N; i++) {
float* row = &mat[ X[i]*M ];
float sum = 0.0;
for(int j=0; j < M; j++) {
if (j < M-32) {
sum += (row[j] + row[j + 32]) / (row[j + 32] + 1.0);
} else {
sum += (row[j] + row[j - 32]) / (row[j - 32] + 1.0);
}
}
row[0] += sum;
}
Remember that row corresponds to a row of matrix
mat as dictated by indirect array X,
hence mat and row are aliased.
We also assume that the compiler could not prove that X
and mat do not alias, and as such TLS needs to be
applied on the accesses of X as well.
Translating a loop for speculative execution requires four steps:
Unified Speculation over A Set of Memory Partitions
The plan is to protect the accesses tomat (and row)
with an in-place TLS instance, i.e., SpLIP, and the accesses to X with
a read-only TLS instance, i.e., SpRO.
To apply speculation (by hand) with PolyLibTLS, we start by constructing the
two TLS instances as below:
const unsigned ENTRY_SIZE = 1;
const unsigned LDV_SZ = logN;
const unsigned SHIFT_FACT = logM;
// 1. HashFunction: hash(a) = ( (a-mat) DIV (2^(SHIFT_FACT+2)) ) MOD (2^LDV_SZ)
typedef HashSeqPow2 Hash;
Hash hash(LDV_SZ, SHIFT_FACT);
// 2. SpLIP protects `mat' and `row'
typedef SpMod_IPcore<Hash> IPm_core;
IPm_core m_core(hash);
typedef SpMod_IP<Hash, &m_core, float> IPm;
IPm ip_m(ENTRY_SZ);
ip_m.setIntervalAddr(mat, mat+N*M);
// 3. SpecRO protects all the other addresses
typedef SpMod_ReadOnly<int> SpRO;
SpRO ro_m;
// 4. Construct the Unified Speculative Memory
typedef USpModel< IPm, &ip_m, IP_ATTR,
USpModel<SpRO, &ro_m, 0, USpModelFP>
>
UMeg;
UMeg umm;
Thread Manager
The next step is to declare the thread manager, which coordinates the execution of speculative (and master) threads and services the rollback-recovery procedure. In the code below, this is achieved by instantiating the abstract classMaster_AbstractTM on several (type) parameters:
const int NUM_THREADS = 6;
const int UNROLL = 1;
class ThManager : public
Master_AbstractTM<ThManager, UMeg, &umm, NUM_THREADS, 0, NormalizedChunks<ThManager, UNROLL> > {
public:
inline ThManager() {
Master_AbstractTM<ThManager, UMeg, &umm, NUM_THREADS, 0, NormalizedChunks<ThManager, UNROLL> >::init();
}
};
ThManager ttmm;
Speculative Thread Interface
The next step is to implement the speculative-thread class that models the implementation of a speculative iteration. With the code below, this comes down to implementing classThread_Max that extends the
speculative-thread skeleton SpecMasterThread. The latter
receives all the information necessary to establish a consistent use of
the thread instance, i.e., the self class Thread_Max,
the thread manager, i.e., ThManager, and the
unified speculative-memory partitions, i.e., UMeg.
The following skeleton-functions require user implementation:
class Thread_Max : public SpecMasterThread< Thread_Max, UMeg, ThManager >
{
private:
typedef SpecMasterThread< Thread_Max, UMeg, ThManager > MASTER_TH;
unsigned long j;
public:
inline Thread_Max(const unsigned long it, unsigned long* dummy) : MASTER_TH(UNROLL,it,dummy){ }
inline void initVars () { this->j = 0; }
inline int end_condition() const { return (this->j >= N); }
inline void updateInductionVars() { this->j = (this->id - ttmm.firstID()) * UNROLL; }
inline int iteration_body() {
unsigned row_nr = umm.specLDslow(&X[this->j], this);
float* row = &mat[row_nr*M];
float sum = 0.0;
for(int i=0; i<M; i++) {
sum += (i < M-32) ?
( this->specLD<IPm,&ip_m>(&row[i]) + this->specLD<IPm,&ip_m>(&row[i + 32]) ) /
( this->specLD<IPm,&ip_m>(&row[i + 32]) + 1.0 ) :
( this->specLD<IPm,&ip_m>(&row[i]) + this->specLD<IPm,&ip_m>(&row[i - 32]) ) /
( this->specLD<IPm, &ip_m>(&row[i - 32]) + 1.0) ;
}
this->specST<IPm, &ip_m>(&row[0], sum);
this->j++;
}
inline int non_spec_iteration_body() {
/* same as iteration_body but with normal read/write accesses */
}
};
The code above shows that there are several ways in which a speculative access can be written, for example:
Starting and Terminating Speculative Execution
Finally, to run the program in speculative mode, one has to:
for (int i = 0; i < NUM_THREADS; i++) {
SpecTh* thr = allocateThread<Thread_Max>(i, 64);
thr->initVars();
ttmm.registerSpecThread(thr,i);
}
gettimeofday(&start, NULL);
ttmm.speculate<Thread_Max>();
gettimeofday(&end, NULL);
running_time = DiffTime(&end_time,&start_time);
Performance Discussion
This section discusses several issues related to the performance of PolyLibTLS. These are demonstrated in the context of our running/motivating example, which was compiled with g++ version 4.4.3 and was run using 6 speculative threads on a quad-core Intel system with hyper-threading support, i.e., Intel(R) Core(TM) i7-2820QM CPU @ 2.30GHz.The implementation of the speculative load/store operations can be tuned via three macros:
When rollbacks are rare, e.g., the elements of
X are
random in the [0..N-1), MACHINE_X86_64 version is about
4x faster than either MODEL_LOCK or MODEL_FENCE
versions, but produces about 2 extra false-positive rollbacks.
The results demonstrates that using CAS locking or memory fences (mfence)
on the critical path of the TLS implementation carries significant,
if not prohibitive, overhead.
When the indirect array
X contains only two distinct elements,
the speculative execution exhibits many rollbacks and the runtime is about
400x slower than the sequential execution (but the result is correct).
When the elements of
X are random in the [0..N-1), then
the speculative execution exhibits the occasional (false-positive) rollback.
The best speculative execution in this case,
i.e., #define MACHINE_X86_64, is only about 1.3x faster
than the original (sequential) runtime,
(and about 4x speedup on a 32-core machine).
However, the speculative code seems to scales well with the hardware parallelism:
This shows reasonable scalability, i.e., 4.5x faster on 6 threads, especially since the system has only 4 physical cores available (with hyper-threading).