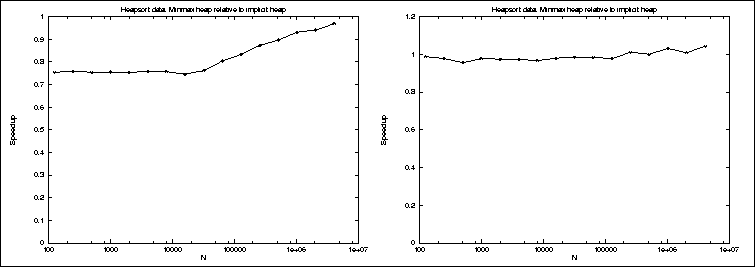
Figure 3.1: Minmax speedup relative to standard heap on P2SC and PPC
The theoretical running time (measured as instruction count) of the minmax heap relatively to the standard heap are according to [4] 7/6 to build the heap, and 5/4 to remove the maximum element from the heap. Removal of the minimum element is done in linear time by the standard heap while the minmax heap handles this case in logarithmic time.
The actual performance of the two heaps has been compared using heapsort.- It does not really make sense to use a minmax heap for sorting since sorting only makes use of the max ordering of the heap, but nevertheless heapsort can be used to measure the penalty for maintaining a minmax heap.
The test was run on two different machines. An IBM F50 with a 332MHz PowerPC cpu, and on an IBM 397 with a 160MHz P2SC cpu. The cache configuration of the PowerPC is 32KB firstlevel cache and 256KB second level cache, while the 397 has a 128KB first level cache only.

Figure 3.1: Minmax speedup relative to standard heap on P2SC and PPC
As is seen in figure 3.1 the theoretical estimate of the relative performance is quite accurate, though somewhat pessimistic. What is more surprising is that the minmax heap is actually faster than the standard heap on the PowerPC for large data sets. The explanation of this anomaly is that even though the instruction count are a bit larger for the minmax heap, the cache behavior is better. A siftdown operation in a minmax heap only accesses the odd levels and the bottom level of the heap. If we assume one cache miss per level for large problem sizes, this cuts the number of cache misses in half. To support this explanation, note that for the P2SC there is a clear break in the curve at 16K elements, which happens to be exactly the size of the cache.