
In the initial presentation of heapsort [8] the heap was build in the obvious way.- The elements to be sorted was inserted into the heap one at a time.
This method has a worst case running time of O(NlogN) and an
expected running time of O(N). The worst case running time is easily
verified.- N-1 iterations are executed. The average tree size is
N/2 elements corresponding to an average tree depth of ![]() .
.
Soon after the first presentation of heapsort an improvement of the heap building procedure was presented in [9] which allows the heap to be build in linear time also in the worst case. The idea is to build the heap starting from the bottom of the tree as seen in listing 2.4.
Since a siftdown run in time O(logN), it is tempting to claim that the algorithm runs in O(NlogN) time, but this argument does not consider that most of the siftdown's are done with a heap size much smaller than N.
If we take an graphical overview of the algorithm this picture is seen:
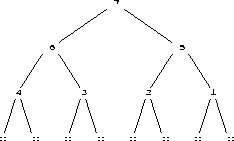
where the subheaps are labeled in the order they are given as parameters to siftdown. Anyway, the correctness of siftdown(i) only depends on the assertions heap(child(i)) and heap(child(i)+1) which gives us the freedom to reorder the calls of siftdown as long as both subheaps of an element are heapified before the element itself.
Now we reorder the siftdowns to
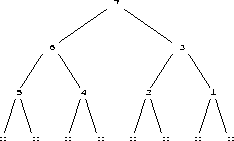
corresponding to the heapify algorithm in listing 2.5.
With this implementation it is easy to see that if we can heapify N elements i time T, the extra work required when the size of the heap is increased to size 2N+1, is only one extra siftdown - running time O(log(2N+1)) - and a heapify of size N. Thus the running time for the total heapify is less than 2T + O(log(2N+1)) which reduces to O(N).
Conventional wisdom is that the bottom up method is faster than the repeated adds method for building the heap, but it is observed in [2] that due to a better cache behavior, the repeated adds method is the fastest for large number of elements.