In order to fully analyse a dice-roll mechanism, we need to have a handle on the probability of the possible outcomes, at least to the extent that we can say which of two outcomes is most likely and if a potential outcome is extremely unlikely. This installment of ``Roll the Bones'' will introduce the basic rules of probability theory as these relate to dice-rolling, and describe how you can calculate probabilities for simple systems. The more complex systems can be difficult to analyse by hand, so we might have to rely on computers for calculations, so we will briefly talk about this too.
Calculating probabilities of dice is both easy and hard: You need only use a few very simple rules to figure out what the probabilities of the possible outcomes are, but for rolls involving many dice or possible rerolls, the calculations may be quite lengthy. In such cases, we can use a computer to do the calculation.
Probabilities usually relate to events: What is the chance that a particular event will happen in a particular situation? Probabilities are numbers between 0 and 1, with 0 meaning that the event can never happen and 1 meaning it is certain to happen. Numbers between these mean that it is possible, but not certain for the event to happen, and larger numbers mean greater likelihood. For example, a probability of ½ means that the likelihood of an event happening is the same as the likelihood of it not happening. This brings us to the basic rules of probabilities:
Two events are independent if the outcome of one event does not influence the outcome of the other. For example, when you roll a die twice, the outcome of the second roll does not depend on the outcome of the first roll (the die doesn't remember the previous roll), so the events are independent. On the other hand, the events ``the die landed with an even number facing up'' and ``the die landed with a number in the upper half facing up'' are not independent, as knowing one of these will help you predict the other more accurately. Taking any one of these events alone (on a normal d6), will give you a probability of ½ of it happening, but if you know that the result is even, there is ⅔ chance of it being in the upper half, as two of 4, 5 and 6 are even.
In the above, we have used an as yet unstated rule of dice: If a die is fair, all sides have the same probability of ending on top. In games, we usually deal with fair dice (all other considered cheating), so we will, unless otherwise stated, assume this to be the case. So, if there are n sides to the die, each has a probability of 1/n of being on top after the roll. The number on the top face or vertex is usually taken as the result of the roll (though some d4s read their result at the bottom edges). Most dice have results from 1 to n, where n is the number of sides of the die, but some ten-sided dice go from 0 to 9 and some are labeled 00, 10, 20, ..., 90. We will use the term dn about a fair n-sided die with numbers 1 to n. When we want to refer to other types, we will describe these explicitly.
If we have an event E, we use p(E) to denote the probability of this event. So, the rules of negation and coincidence can be restated as
| p(not E) | = | 1 - p(E) |
| p(E1 and E2) | = | p(E1) × p(E2) |
We can use the rules of negation and coincidence to find probabilities of rolls that combine several dice. For example, if you roll two d6, the chance of both being sixes (i.e., rolling ``box cars'') is 1/6×1/6 = 1/36.
But what about the probability of rolling two dice, such that at least one of them is a six? It turns out that we can use the rules of negation and coincidence for this too: The chance of having at least one die land on a six is 1 minus the chance that neither land on sixes, and the chance of getting no sixes is the chance that the first is not a six times the chance that the other is not a six. So we get 1-5/6×5/6 = 11/36. We can calculate a general rule as
| p(E1 or E2) | = | 1 - p(not(E1 or E2)) |
| = | 1 - p(not(E1) and not(E2)) | |
| = | 1 - p(not(E1)) × p(not(E2)) | |
| = | 1 - (1 - p(E1)) × (1-p(E2)) | |
| = | p(E1) + p(E2) - p(E1) × p(E2) |
For another example, what is the chance of rolling a total of 6 on two d6? We can see that we can get 6 as 1+5, 2+4, 3+3, 4+2 and 5+1, so a total of 5 of the possible 36 outcomes yield a sum of 6, so the probability is 5/36. Note that we need to count 1+5 and 5+1 separately, as there are two ways of rolling a 1 and a 5 on two d6, unlike the single way of getting two 3s.
In general, when you combine several dice, you count the number of ways you can get a particular outcome and divide by the total number of rolls to find the probability of that outcome. When you have two d6, this isn't difficult to do, but if you have, say, five d10, it is unrealistic to enumerate all outcomes and count those you want. In these cases, you either use a computer to enumerate all possible rolls and count those you want, or you find a way of counting that doesn't require explicit enumeration of all possibilities, usually by exploiting the structure of the roll.
For simple cases, such as the chance of rolling S or more on x dn, some people have derived formulae that don't require enumeration. These, however, are often cumbersome (and error-prone) to calculate by hand, so you might as well use a computer. For finding the chance of rolling a sum of 15 or more on 3d6, we can write the following program (in sort-of BASIC, though it will be similar in other languages):
count = 0
for i1 = 1 to 6
for i2 = 1 to 6
for i3 = 1 to 6
if i1+i2+i3 >= 15 then count = count + 1
next i3
next i2
next i1
print count/216
Each loop runs through all values of one die, so in the body of the innermost loop, you get all combinations of all dice. You then count those combinations that fulfill the criterion you are looking for. In the end, you divide this count by the total number of combinations (which in this case is 63 = 216).
Such programs are not difficult to write, though it gets a bit tedious if the number of dice can change, as you need to modify the program every time (or use more complex programming techniques, such as recursive procedure calls or stacks). To simplify this task, I have developed a programming language called Troll specifically for calculating dice probabilities. In Troll, you can write the above as
sum 3d6
and you will get the probabilities of the result being equal to each possible value, as well as the probability of the result being greater than or equal to each possible value. Alternatively, you can write
count S<= (sum 3d6)
which counts only the results that are at least S. You can find
Troll, including instructions and examples, at http://hjemmesider.diku.dk/~torbenm/Troll.
If you can assign a value to each outcome, you can calculate an average (or mean) value as the sum of the probability of each outcome multiplied by its value. More precisely, if the possible outcomes are E1,...,En and the value of outcome Ei is V(Ei), then the average of the outcomes is p(E1)×V(E1) + ··· + p(En)×V(En). For a single d6, the average is, hence, 1/6×1 + ··· + 1/6×6 = 21/6 = 3.5. In general, a dn has average (n+1)/2.
If you add several dice, you also add their averages, so, for example, the average of x dn is x × (n+1)/2.
In addition to the average of the outcomes and the range of possible values, it is often interesting to know how far outcomes are likely to be from the average. There are various measures of this, the simplest being the mean deviation, which is the average distance from the mean value. While conceptually simple, mean deviation is difficult to work with, so you often use variance or spread (also called standard deviation) instead. I will not go into detail about how these are calculated, only note that the spread is typically close to (and a bit larger than) the mean deviation, and that the variance is the square of the spread. You can read more at MathWorld.
Troll can calculate the average, spread and mean deviation of a roll.
The rules above can be used to calculate probabilities and mean of any finite combination of dice (though some require complex enumeration of combinations). But what about open-ended rolls, i.e., rolls that allow unlimited rerolls of certain results? There is no way we can enumerate all combinations, so what do we do?
A simple solution it to limit the rerolls to some finite limit and, hence, get approximate answers (Troll, for example, does this). But it is, actually, fairly simple to calculate the average of a roll with unbounded rerolls.
Let us say that we have a roll that without rerolls has average M0, that you get a reroll with probability p and that when you reroll, the new roll is identical to the original (including the chance of further rerolls) and added on top of the original roll. This gives us a recurrence relation for the average M of the open-ended roll: M = M0 + p*M, which solves to M = M0/(1-p).
For an n-sided die with values x1,...,xn, and rerolls on xn, this yields M = (x1+···+xn)/(n-1), where the average without reroll is (x1+···+xn)/n.
As an example, let us take the dice-pool system from White Wolf's ``World of Darkness'' game. In this system, you roll a number of d10s and count those that are 8 or more. Additionally, any 10 you roll adds another d10, which is also rerolled on a 10 and so on.
Without rerolls, the values are x1,...,xn = 0,0,0,0,0,0,0,1,1,1. So the average of one open-ended die is (0+0+0+0+0+0+0+1+1+1)/(10-1) = 3/9 = 1/3. If you roll N WoD dice, the average is N/3.
When talking about distribution of results (such as dice rolls), people often use the term bell curve to mean that the distribution looks somewhat like this:

I.e., reminiscent of a normal distribution. Strictly speaking, dice rolls have discrete probability distributions, i.e., the distributions map to bar diagrams rather than continuous curves, so you can't strictly speaking talk about bell curves. Additionally, mathematicians usually reserve the term ``bell curve'' for the normal (or Gaussian) distribution p(x)=e-x2, which is only one of may bell-shaped curves.
With discrete distributions, you can have bar diagrams that are approximately bell shaped (as does, for example, the classical 3d6 distribution below) and call these ``bell curves''.
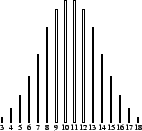
Many people use ``bell curve'' also when referring to non-symmetric distributions, such as the one you get for the sum of the three highest of four d6 (as used in d20 character generation), though such strictly speaking aren't bell curves in mathematical terms. I will, like most gamers, use ``bell curve'' in this loose sense, but specify when bell-like distributions are non-symmetric.
The main use of bell curves in RPGs is in generating attributes — since ``real world'' attributes supposedly follow normal distributions, people want this to be true in the game also. However, this is relevant only insofar as the in-game attributes translate linearly into real-world values. While this may be true for height and weight, etc., there is no indication that, for example intelligence in a game translates directly to IQ (which is defined to follow a normal distribution centered on 100). You can also argue that when the same person performs the same task repeatedly, the distribution of results resembles a normal distribution, so you ought to use a bell-curved dice roll for action resolution. But again, this requires that the quality of results in the game translates linearly to some real-world scale, which is not always the case. For example, if a game uses a logarithmic scale on attributes or results, using a normal distribution of attributes doesn't seem right. I'm not saying that using bell curves is a bad thing, but that you should not use them indiscriminately.
In the next couple of installments, I will look at some common dice-roll methods and discuss their properties.